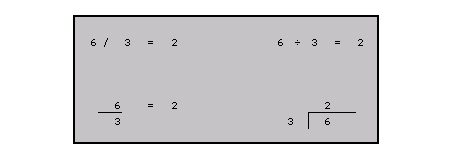
Division

Scroll down for further teaching material and practice exercises.

Video

Division Instruction

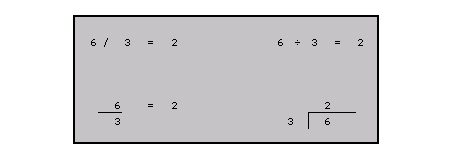
The above equations have the same values and are very straightforward. It is important to know that the order of the numbers is significant in division (and subtraction). Different ordering of numbers will result in different answers. For example:

Simply put, division determines how many times a number will fit into another. Picture an auditorium with 100 chairs available. Several schools want to send 20 students to see a play in the auditorium. Now you need to determine how many schools can attend the play. This will require division.

By dividing 100 by 20 (100 ÷ 20) you come up with the number 5. Five schools can send 20 students to attend the play.

Long Division

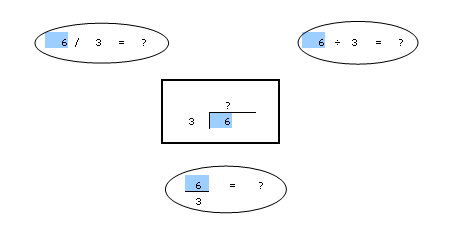
When performing long division, it is important to organize the information as is seen in the centre square. You have to understand how the different formats for division are transferred into the format seen above.

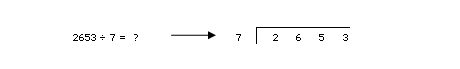
In order to answer a division question on paper, you must place the equation in the proper format. After this is accomplished you can begin to solve the problem.

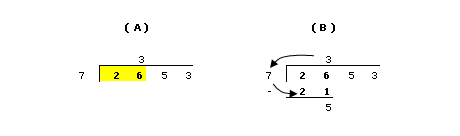
(A)
The first step is to focus on the highlighted area of the number under the bracket. You have to work with a number that is larger than the dividing number (7). Because 2 is smaller than 7, you have to work with 26. Ask yourself how many times you can multiply 7 without going over 26. If you count by 7's (7, 14, 21, 28) you'll realize that 3 is the most times that 7 will fit into 26.

(B)
With the information you have in section A, you now have to perform a simple multiplication. Take the top number (3) and multiply it by the dividing number (7). The answer is placed below the and then subtracted from the digits you were working with. (26 - 21 = 5) Make sure you keep the numbers in the proper columns. (If, after subtracting, the answer is greater than the dividing number you need to start again, using a larger top number.)

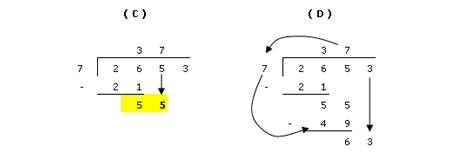
(C)
After subtraction, bring down the next digit to sit beside the solution. This becomes your new number to work with (55). Then repeat step A using this number. Determine how many times you can multiply 7 without exceeding 55. Place this digit above the next digit in the question on top of the bracket.

(D)
Next repeat step B. Multiply out the 7's and record your answer below the 55. Subtracting the numbers results in 6. Continue to work the same pattern, and bring down the next digit in the question to determine a new number to work with.

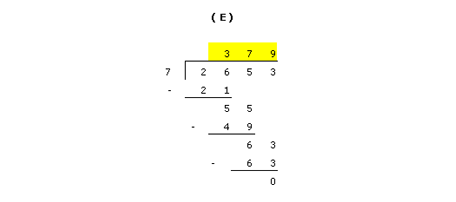
(E)
The final steps in the process are to repeat the process. Determine how many times you can multiply 7 without going over 63. You can do this 9 times. When you multiply it out and subtract the result is 0. The answer to the question is highlighted on top.

2653 ÷ 7 = 379

Decimals

There are times when you are dividing a number and on the final subtraction, there is a value left over. This is a remainder. When this happens, you can choose whether or not to continue calculating the number. If you continue, 1 or more decimal points will be introduced. For example:

You must follow the same procedure with decimal places as you would with regular long division. Ensure that the digits are properly lined up, and continue adding 0's after the decimal places in the equation.

Decimals and Whole Numbers

You may be required to solve division problems with decimals. Below are two examples of decimals occurring in division questions.

Example 1

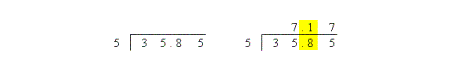
To answer the question correctly, you have to place the decimal point in the answer directly above the decimal point in the question.

Example 2

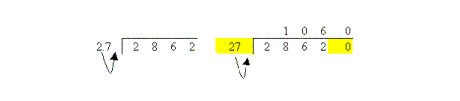
When a decimal point is found in the denominator (the number of parts into which the whole is divided – bottom number of a fraction), then you must eliminate it before answering the question. This is achieved by shifting the decimal point however many spaces to the right it takes to create a whole number, in this example one space. This has to be matched by shifting the decimal place in the numerator (the number to be divided – top number of a fraction) by one space as well. If the numerator is a whole number, shift the decimal point right by adding a zero as in the example above.

Example 3

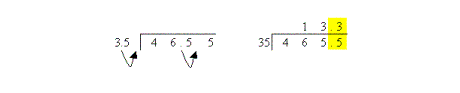
When a decimal point is found in both the numerator and the denominator you must combine both steps. First, you must eliminate the decimal place in the denominator, as in example 2. Then you have to ensure that the new decimal place lines up, as in example 1.

Hints

Long division becomes more complicated with higher numbers, especially higher denominators.

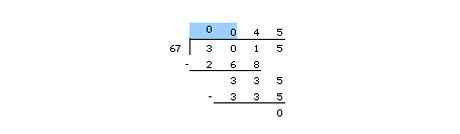
Using 0's to Line up Numbers
67 will not fit into 3, or 30. You will therefore have to work with 301. By placing 0's above the 3 and the 0, (highlighted), you will not make any errors with improperly aligned numbers.

Rounding Up
Determining how many times 67 will fit into 301 can be a difficult task. It may help to round 67 up to 70. By counting 70 four times, you will reach 280. Five times equals 350, which exceeds 301. Four is the best guess, and by multiplying it out, using 67 you are proven correct.

Disregarding Decimals
The majority of the answers on a police test will not require decimals. If your calculation of an equation gives you an answer with decimals, but none of the optional answers have decimals, stop calculating. Make a selection from the available options, or consider that you made a mistake. Quickly check your work, but don’t spend too much time on one question that’s causing you problems. Move onto the next one.

Zeros and Ones
Any time zero is divided by any other number the answer is 0.

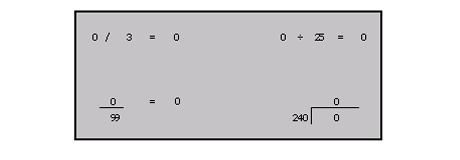
It is impossible for a number to be divided by 0. It is indefinable.

Any number divided by 1 is equal to itself.

Practice Questions

Try these practice questions. The answers are posted below.

a) 49 / 7 =

b) 78 / 13 =

c) 225 / 9 =

d) 152 / 8 =

e) 702 / 9 =

f) 441 / 21 =

g) 533 / 13 =

h) 455 / 7 =

i) 1452 / 66 =

j) 1071 / 17 =

Answers

a) 7
b) 6
c) 25
d) 19
e) 78
f) 21
g) 41
h) 65
i) 22
j) 63